Cognitive science may have become possible in part because Alan Turing had terrible handwriting. To explain why this is so requires a somewhat complicated story, the telling of which is the purpose of this chapter. Along the way, I also hope to tell you why the assumption that intelligence is the result of information processing makes conversation among cognitive scientists possible.
TURING MACHINES AND COGNITIVE SCIENCE
Mathematical Foundations
Galilleo said that the book of Nature is written in the language of mathematics, and I see no reason to disagree. This should make it no surprise that the answer to a fundamental question in mathematics led directly to the origin of cognitive science.
Mathematics is a formal system built from the ground up. Mathematicians begin with a set of statements, called axioms, that are assumed to be true. They then propose (and apply) particular rules to these axioms. These rules allow them to deduce new facts that are guaranteed to be as true as the axioms. As a result, these new facts can also become the source of further theoretical statements. The result is that a complete mathematical theory can be "grown" by making deductions from the initial assumptions. For example, the entire formal structure of arithmetic, including the many different kinds of number systems, can be derived from the axioms of set theory (e.g., Stewart & Tall, 1977).
One important problem with axiomatic systems concerns the truth of the initial assumptions. Generally, mathematicians start with axioms that appear to be obviously true. Nevertheless, this still means that the entire foundations of mathematics rest on a set of shared intuitions. This is not the most comforting thought, for if it is later discovered that an "obviously true" axiom is actually false, then the entire superstructure of mathematics would come crashing down.
At the turn of the 19th century, the German mathematical giant David Hilbert decided that the intuitive basis of mathematics could be replaced with cold, hard, irrefutable truth. He launched a research program to establish the absolute foundations of mathematics. Hilbert proposed a number of precise questions about the fundamental nature of mathematics. He believed that mathematics did indeed have an absolute foundation, and that as a result the answer to all of his questions would be "yes". Thus for Hilbert, these questions represented a few loose ends for the field to tie up. For other mathematicians, these questions represented a challenging puzzle whose solution would validate the entire discipline. Unfortunately for the Hilbert program, by the early 1930s mathematicians had shown that the answers to many of Hilbert's key questions were actually "no", and as a result an absolute basis for mathematics was not possible.
The Entscheidungsproblem
Interestingly, the negative answer to one of Hilbert's questions, the Entscheidungsproblem, had enormous positive consequences in nonmathematical arenas, and eventually led to the development of cognitive science. The Entscheidungsproblem was this: Is mathematics decidable?
Mathematics has been described as the branch of philosophy most interested in questions concerning formal logic. From this perspective, any statement in mathematics can be viewed as a sentence or expression written in a logical notation. If mathematics was decidable, then in principle there existed a "definite method" that would work as follows: One could write any mathematical expression, and then apply this definite method to it. The method would be guaranteed to decide whether the expression was true or false. In short, the definite method would be a mechanism for determining the truth or falsehood of any mathematical claim.
Difficulties in answering the Entscheidungsproblem emerge because it appears to require that two very contradictory conditions be met. On the one hand, the definite method has to be extraordinarily general and powerful. This is because the method must be capable of dealing with any mathematical expression. On the other hand, the method has to be exceptionally simple, so that mathematicians will agree about its suitability for claims about decidability. In other words, to solve this problem, a mathematician would have to propose an extremely simple information processing mechanism capable (in spite of its simplicity) of resolving exceptionally complicated mathematical expressions. To prove that no such method could exist for all expressions, the British mathematician Alan Turing had to invent the basis for modern computers (Turing, 1936).
The Supertypewriter
From his early days in school, Alan Turing had been plagued with horrible handwriting. His teachers' reports included such chestnuts as "I can forgive his writing, though it is the worst I have ever seen, and I try to view tolerantly his inexactitude and dirty, slipshod work" (Hodges, 1983, p. 30) and "his handwriting was so bad that he lost marks frequently -- sometimes because his work was definitely illegible, and sometimes because his misreading of his own handwriting led him into mistakes" (p. 38). Even as a child, though, Turing fought back against this liability. In April of 1923 (when he was only 11) he wrote a letter using a less-than-successful fountain pen that he had invented, and a few months later another of his letters "described an exceedingly crude idea for a typewriter" (p. 14).
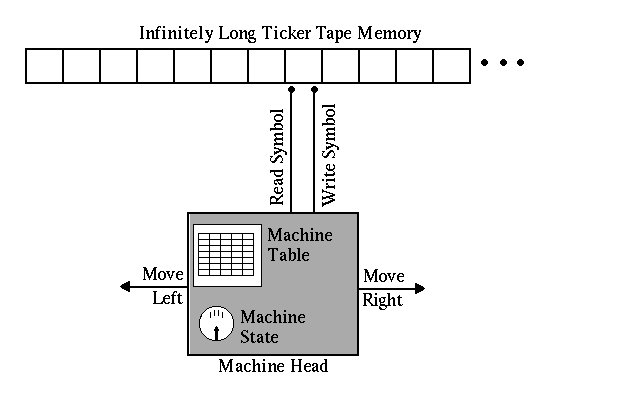
This childhood fascination with writing machines may have played an important role in an older Turing's thoughts about a definite method for resolving the decidability question (for a detailed development of this view, see Hodges, 1983, pp. 90-102). Turing realized that a typewriter had many of the characteristics that would be required of a general purpose information processor. First, it essentially had an infinite memory. Its continually replaced sheet of paper was reconceived by Turing as an infinitely long ticker tape. Second, it could move back and forth along this paper, at any time pointing to a particular location on the sheet. Turing proposed that the ticker tape of his machine was divided into small cells, at that at any particular time, only one of these cells would be processed. Third, the typewriter could write a symbol to its memory. Fourth, this writing was a definite act that depended upon a machine configuration. For instance, in the regular physical state of the typewriter, if one pressed a specific key the symbol "q" was written. However, if the physical state of the typewriter was changed by pressing the "CAPS LOCK" key down, pressing the same key would produce a different symbol, "Q".
Turing produced his definite method by adding some additional properties to his machine, making a `supertypewriter'. First, he gave it the ability to read the symbol in the memory cell that it was processing. Second, he gave it the ability to erase the symbol in the current cell (i.e., by writing a special BLANK symbol). Third, he allowed it to have many different physical configurations, although this number was required to be finite to ensure that the machine was really definite.
The resulting device is now known as the Turing machine, and Figure 2.1 presents one manner in which such a machine can be illustrated. The machine itself is separated into two different components, the infinitely long ticker tape which serves as a memory and the machine's head which manipulates the memory. The memory is divided into a series of cells, any one of which can only contain a single symbol. The head includes mechanisms for moving left or right along the tape (one cell at a time), for reading the symbol in the current cell, and for writing a symbol into the current cell. The head also includes a register to indicate its current physical configuration or machine state. Finally, the head includes a set of basic instructions, the machine table, which precisely defines the operations that the head will carry out.

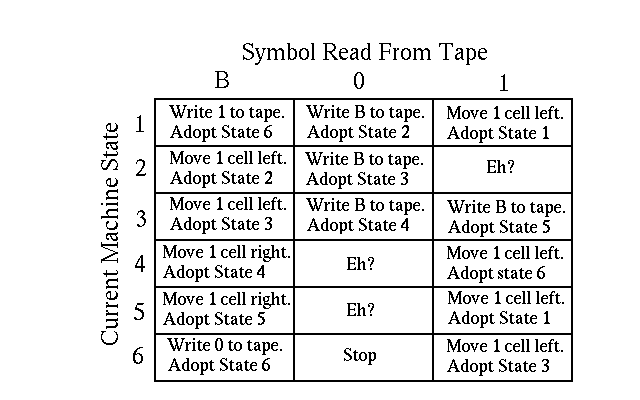
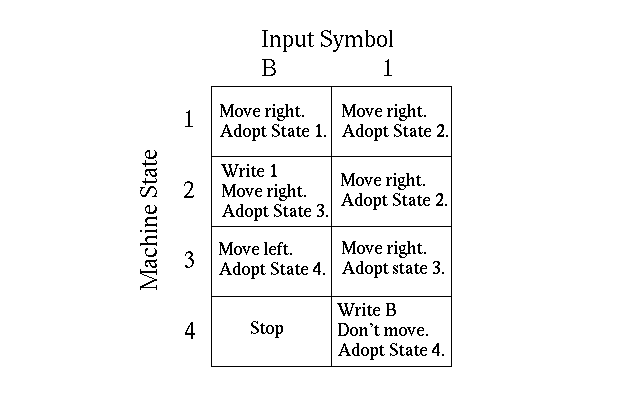
Figure 2.2 illustrates an example machine table for a particular Turing machine. The table has six different rows, because this particular machine will at any time be in one of six possible machine states. The table has three columns, because at any particular time it will be reading only one of three possible symbols on the tape: a blank ("B"), a "0", or a "1". Each entry in the table consists of a simple instruction to be carried out when the Turing machine is in a specific state and is reading a specific symbol. Most of the instructions involve either writing a particular symbol to the tape, or moving one cell to the right or to the left. All of these instructions also involve adopting a specific machine state. There are a couple of other instructions of note on the table as well. For instance, at Row 4 and Column 0 the table says "Eh?". This simply means that some mistake has been made, because this particular machine should under normal circumstances be in state 4 while reading the symbol "0". At Row 6 and Column 0 the table says "Stop". When the machine carries this instruction, it simply stops processing, because it has completed the task that it was programmed to do.
How does a Turing machine actually work? Essentially, a programmer writes a particular question on the tape in symbols that the machine recognizes. Then, the programmer places the Turing machine at a particular cell on the tape in a starting machine state (usually state 1). Then the machine begins to follow its machine table, moving back and forth along the tape, usually rewriting it as it goes. Finally, the machine executes its "Stop" instruction, and quits moving. At this point, the symbols written on the tape represent the machine's answer to the original question.
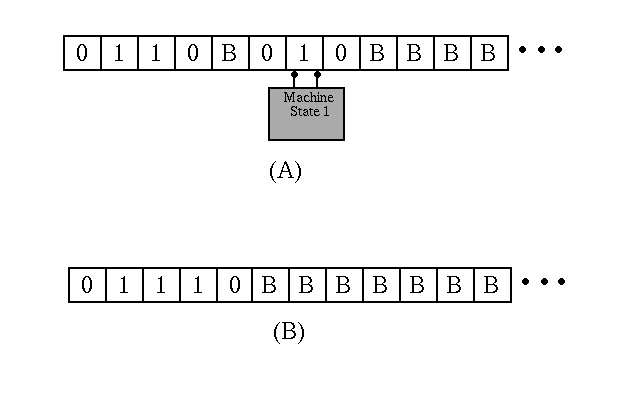
For example, imagine that the Turing machine described in Figure 2.2 was placed in machine state 1 on the tape drawn in Figure 2.3a. The really interested reader could pretend to be that machine, working along the tape following the instructions in the table. To do this, it would be useful to have available a little scratch pad to keep track of the current machine state. At the end of this exercise, the machine will "Stop", and the answer to Figure 2.3a's question is the tape illustrated in Figure 2.3b. (Before reading on, stop to consider this: there is no doubt that you would have no difficulty in pretending to be this particular Turing machine, and that by following your Figure 2.2 program you could generate the correct answer to the question in Figure 2.3a. But can you tell me right now what this answer means, or even what you think the original question is?)
In general, Turing machines can be built to answer a diversity of questions. For example, a Turing machine can compute functions from integers to integers. So, if you were to write an integer value down in some notation on the tape, a Turing machine computing a particular function would write the function's value for that integer on the tape and then halt. Such a function is called a partial recursive function. If the Turing machine is guaranteed to halt for any input when it computes its function (i.e., if it is guaranteed to keep out of an infinite loop of moving back and forth along the tape), then it is computing a total recursive function. All common arithmetic operations on integers are total recursive functions. As another example, a Turing machine can accept or reject a string of symbols as representing a sentence belonging to a language. Such a language is called recursively enumerable. If the Turing machine is guaranteed to halt for the language that it "knows", then the language is said to be recursive. The set of recursive languages includes context-free grammars, which have been used to model the syntactic structure of natural human languages.
The Universal Machine
Any reader who took the trouble to pretend to be the Turing machine in Figure 2.2 should realize that he or she is a particularly powerful computing device. This is because they would have absolutely no difficulty simulating any machine table that I could have decided to put in this figure. In short, the reader can be thought of as a universal machine, capable of carrying out the operations that define any Turing machine.
Amazingly, it is possible to build special Turing machines that are themselves universal machines. This is accomplished by creating an important qualitative distinction in the machine's tape between data that is to be manipulated and a program that is to do the manipulating. Figure 2.4a illustrates this kind of distinction. For a Universal Turing machine (UTM), the first part of the tape provides a description of some Turing machine T that is to operate on some data. This description is essentially the stringing out of machine T's table (see Figure 2.4b) in a format that can be read by the UTM's tape head (for one sample notation, see Minksy, 1963, Section 7.2). The next part of the tape provides a small number of cells to be used as a scratch pad. The final part of the tape is the actual data, representing the question that machine T is supposed to answer.
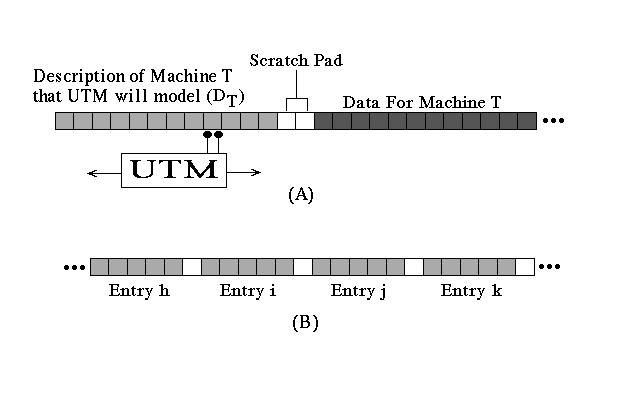
A UTM works in a fashion very analogous to the reader simulating the machine in Figure 2.3, moving back and forth between the machine description and the data, keeping track of important information (like the current machine state) in the scratch pad. Essentially, the UTM reads a data symbol, goes back the the machine description to find out what machine T (in its current state) would do after reading that symbol, and then goes back to the data tape and performs this operation. The UTM itself is defined as a machine table capable of reading and acting out machine T's description, and need not be a particularly complicated looking device.
Why Is Cognitive Science Interested In Turing Machines?
To summarize a few things to this point, we have described a Turing machine as a device that uses a machine table to answer questions written on a data tape (essentially by rewriting the tape). In addition, special Turing machines (UTM's) have the ability to pretend to be any possible Turing machine. Thus a single UTM can answer any question that can be answered by a Turing machine. An important question remains: Why in the world would cognitive science be interested in these kinds of machines? The answer to this question really depends on the answers to three related issues.
1) How well do Turing machines describe information processing? Cognitive science is extremely serious about its view that cognition is information processing. "For me, the notion of computation stands in the same relation to cognition as geometry does to mechanics: It is not a metaphor but part of a literal description of cognitive activity" (Pylyshyn, 1979, p. 435). Given this view, we can ask the extent to which a Turing machine provides a faithful account of what information processing is all about. The answer to this question is surprisingly strong: a Turing machine gives a complete account of what information processing is all about.
According to what we will call the Church-Turing thesis, "Any process which could naturally be called an effective procedure can be realized by a Turing machine" (Minsky, 1963, p. 108). This thesis cannot be proven because of the intrinsic ambiguity of the term "naturally". However, most researchers accept this thesis as being true. This is because it has been shown that all other accounts of what an effective procedure (or an information processor) is, though at first glance often quite different in appearance from Turing's proposal, have been shown to be formally equivalent to a Universal Turing machine. In short, a Universal Turing machine is the most powerful description of information processing we have, because anything that can be computed could be computed by this device.1
2) Can Turing machines answer psychologically interesting questions? A second question that must be answered in order to understand cognitive science's interest in Turing's work concerns the competence of a Universal Turing machine -- when we write queries on the ticker tape for the machine to answer, what kinds of questions can we ask? More to the point, is there any reason to believe that the kinds of questions that a Turing machine can answer might be of psychological interest? Again, the answer to this question is far from univocal -- if we had a definite answer, either cognitive science would be either complete (because we would have found a way to make a thinking machine) or abandoned (because we would have found that the information processing hypothesis is wrong). Nevertheless, there are many indications that the Turing machine's competence is sufficiently powerful to be of psychological interest. We have already defined a UTM as being able to compute any partial recursive function, or to determine the acceptability of a recursively enumerable language. I'd like to change gears a little bit from this, and consider a specific example of relating a machine's competence to some psychologically relevant issues.
One of the kinds of questions that can be given to computing devices concerns the acceptability of sentences. For this type of question, you write a sentence in some language (usually an artificial one) on the machine's tape, and then start the machine running. At the end, the machine is supposed to tell the user whether the sentence is a valid or grammatical example of a specific language.
Bever, Fodor, and Garret (1968) were concerned with an extremely simple looking artificial grammar, whose sentences were made entirely from the following two "words": "a" or "b". Here are some valid sentences created from this grammar: "a", "bab", "bbabb", and so on. Here are some ungrammatical sentences that are inconsistent with this grammar: "ab", "babb", "bbb", and "bbabbb". From this information, would you agree that "bbbbbabbbbb" is a grammatical sentence in this language? It is, because this string can be generated by the rule that defines this "mirror image" language, bNabN where N is the number of "b's" in the string.
Bever, Fodor and Garret (1968) were able to show that a particular computational device, called a finite state automaton, could not correctly decide whether strings of "a's" and "b's" were acceptable according to their simple grammar. A finite state automaton is similar to a Turing machine, but has less computational power. This is because it can only move in one direction along a tape, and can only read tape symbols. It doesn't write to the tape -- it only stops at the end of a sentence, finishing in a physical state that means (for our example) either "yes it's grammatical" or "no it's not grammatical". Because it can't go backwards along the tape, it can't deal with languages (like the artificial mirror image one) that have embedded clausal structure.
The reason that this proof is so powerful is because Bever, Fodor and Garret argued that the finite state automaton had essentially the same computational power of a device guided by the principles underlying associationism (not to mention radical S-R behaviorism). Their message was clear: associationism wasn't powerful enough to deal with the embedded clauses of natural human language, because a finite state automaton wasn't powerful enough to deal with even an extremely simple language in which clauses could be embedded. As a result, associationism should be abandoned as a theory of mind. The impact of this proof is measured by the lengthy responses to this argument by memory researchers with strong associationistic tendencies (for examples see the responses to the so-called "terminal metapostulate" in Anderson & Bower, 1973; Paivio, 1986).
In contrast, Turing machines can decide the acceptability of sentences created from grammars that can generate embedded clauses. So, a Turing machine could (like the reader) make the correct judgement about the string "bbbbbbabbbbbb" for the artificial language that was described earlier (for additional discussion, see Johnson-Laird, 1983, Chap. 12). This suggests that it provides a framework for cognitive science that may be sufficiently rich to provide accounts of human cognition. Turing himself was convinced about the inevitability of machine intelligence, and in one extremely influential paper he described an empirical method for identifying it (Turing, 1950).
3) From the finite to the infinite. There is one final note to make about cognitive science's interest in Turing machines before we move on to other issues. Like the decidability question, the notion of human intelligence appears to pull us in competing directions. On the one hand, we have a strong intuitive sense that human intelligence is unlimited; as far as we are concerned, it has no bounds, and is capable of producing an infinity of products (sentences, ideas, works of art, and so on). On the other hand, we also have a strong belief that mechanically speaking human intelligence is quite limited. In general, most people would agree with Searle's (1986, 1990) proposal that brains cause minds, and recognize that brains are not infinite or magical devices. How is it possible for three pounds of flesh and blood to instantiate human intelligence?
A Universal Turing machine provides one approach to resolving this conundrum because it is inherently componential in nature. On the one hand, such a machine is definitely finite in structure. On the other hand, the machine has an incredibly large potential repetoire of behaviors. This is possible because the machine does not have to understand any question written on the ticker tape as a whole. Instead, the machine breaks the question down into meaningful chunks or components -- the individual symbols written on the tape -- which it does "understand", at least to the extent that it will carry out a specific operation according to its machine table. The power of the Turing machine comes from the fact that if you take a small number of simple, basic information processing operations (i.e., machine table actions) and string them together in a specific sequence, very complicated behaviors can emerge.
Human language can be viewed as providing another example of the computational power that can emerge from componential systems. Human language appears to have limitless novelty. We apparently have no problem whatsoever producing novel sentences, utterances which have never before been seen or heard on this planet. (Sentences like "My dog would make a fine mascot for the Montreal Canadiens.") Not only is the production of such sentences fairly straightforward, but the amazing thing is that when they are heard or read by others, they are easily understood in spite of their novelty. However, this may be the result of the fact that with a finite number of words (the documentation for my wordprocessor says that its spellchecker contains about 140,000) and a finite number of rules for putting them together sensibly, there is essentially no restriction on the number of different sentences that the human race can produce. Furthermore, if someone reading or hearing a novel sentence knows something about the meanings of the components of the sentence, as well about the rules for putting these components together, it becomes a little less surprising that they can understand what was being said.
WHAT CAN YOU SAY ABOUT A TURING MACHINE?
To this point in this chapter, we have described some of the basic properties of information processing from the Turing machine perspective. We have also briefly considered why cognitive science is interested in Turing machines. What we have not covered yet, though, is how viewing information processing from this perspective affects basic research in cognitive science. It turns out that by considering briefly the different ways in which we can explain the behavior of a Turing machine, we can begin to see a number of fundamental properties of cognitive science, and to understand where these properties come from. The remainder of this chapter is going to argue that as soon as you take seriously the hypothesis that the mind is an information processor, then you also have to take seriously several other claims. First, in order to have a complete explanation of mental processes, you will be forced to describe them using several qualitatively different vocabularies, each of which captures different (but important) regularities. Second, in addition to coming up with these qualitatively different descriptions, you will have to come up with some relationships between them -- after all, they are all describing the same system. Third, for complex systems (like biological organisms), these vocabularies are going to be so different, and so difficult, that it is unlikely that one researcher will be technically competent to deal with them all. As a result, a number of different researchers, each with quite different kinds of expertise, will be required to provide these different descriptive accounts and to provide the links between them. In short, the interdisciplinary nature of cognitive science is a necessary consequence of adopting the information processing hypothesis!
To start to get a handle on this perspective, imagine that our goal is to provide some account of a Turing machine. What different kinds of things might we say about it? How are these different accounts related to one another? Let's start at the most concrete level, and then work our way up to more abstract descriptions.
Physical Descriptions
In order to make claims pertaining to the decidability problem, Turing did not have to actually build his "supertypewriter". One reason for this was the astonishing simplicity of the machine, which permitted Turing to make claims about its ability without requiring them to be defended empirically. A second reason was the fact that Turing was doing mathematics, not computer science. What was important was an abstract description of what an effective procedure was, not a piece of hardware capable of performing such a procedure. A third reason was the obvious inefficiency of the device -- Turing machines are remarkably slow, even for very simple computational tasks. Interestingly, this was also true of the first electronic computers. For instance, Turing was a key figure in the development of working computers in the United Kingdom, and was also the author of some of the first chess-playing programs. However, Turing did not test these programs on the machines that he was developing because they were too limited in speed and memory. "Alan had all the rules written out on bits of paper, and found himself very torn between executing the rules that his algorithm demanded, and doing what was obviously a better move (Hodges, 1983, p. 440).
All of this aside, if we wanted to, we certainly could build a Turing machine. This would be a mechanical device that would process a ticker tape memory in a manner consistent with a particular machine table. We could give it some sample problems on a ticker tape, watch it process the tape, and then check its answers to ensure that this particular physical device was functioning according to its design.
After building this machine, if someone asked how it worked, then one perfectly valid answer would be a physical description of the thing that we had built. We could describe the mechanical processes involved in moving along the tape, involved in reading symbols, and in writing new symbols to the tape. We could explain the mechanisms for switching from one machine state to another. We could provide some physical measurements of the machine -- how much it weighed, how long it took to move from one tape cell to the next, how much heat it generated as it worked. Thus it seems pretty plain that one kind of vocabulary that can be applied to information processors is a description of their physical or mechanical characteristics.
This kind of vocabulary has several advantages. For example, when you describe things physically, then you can make certain predictions about their performance that you would likely not be able to make had you used any other kind of description. For example, if our physical Turing machine was powered by alkaline batteries, then physical descriptions would allow us to predict that its performance would decrease over time because of a decrease in terminal voltage of the battery (e.g., Boylestad, 1990, Figure 2.16) and to predict that its performance would be poorer in colder temperatures because of a temperature-related decrease in battery capacity (e.g., Boylestad, 1990, Figure 2.15b).
From psychology's standpoint, physical descriptions are particularly alluring because they give a strong sense of grounding relatively weak psychological theory in the established foundations of harder and more respected sciences.2 Recent advances in the neurosciences make biological accounts of psychological processes particularly seductive. For instance, it is amazing these days the extent to which researchers can relate behaviorally interesting claims about memory to underlying neural circuitry, not to mention mechanisms described quite literally at the molecular level (e.g., Alkon, 1987; Lynch, 1986). It is small wonder that some philosophers are of the opinion that as neuroscience develops, the folk psychology that we use everyday to predict the behavior of others will evolve into a more precise and effective folk physiology (e.g., Churchland, 1988, pp. 43-45). For our purposes, though, it is critically important to realize that physical descriptions, while extremely powerful, are not complete.
Limitations Of Physical Descriptions
One kind of incompleteness involves what philosophers call the multiple realization argument. Essentially, what this means is that you could build many qualitatively different physical devices that all instantiated the same information processing device (e.g., the same Turing machine). A physical description of one of these devices would tell you nothing about any of the others. A very nice real world example of this has recently come to light. Researchers in the United Kingdom have successfully built Charles Babbage's analytic engine (Swade, 1993). This device is a machine that, like modern computers built from silicon technology, has the same computational power as a UTM (Haugeland, 1985). However, unlike modern computers, the analytic engine is like a beautiful clock, with rotating cylinders used to represent floating point numbers, and with computation carried out by physically turning a crank which rotates these cylinders via a system of gears. Obviously, information processing devices share certain abstract properties that are not captured in purely physical descriptions.
Physical accounts of information processing systems are limited by another consideration as well. Consider this beautiful story provided by Arbib (1972, pp. 11-12): In December 1966, the computer science department at Stanford University installed a new computer. Unfortunately, the computer arrived without its instruction manuals. Undaunted, a group of graduate students decided that they didn't need these manuals, and attempted to deduce enough information about the computer's structure to write meaningful programs. Given that these students knew that this device was a digital computer, and had loads of experience with other computers, they quickly located the power switch, the data entry switches, and some important control push buttons. They were soon able to enter and execute some basic instruction words -- but that was about it. "In several hours of experimentation we completely failed to deduce such simple items as the format of the instruction word (or even the location of the op-code). We were unable to program the addition of two numbers or the simplest input-output." These difficulties were assumed by the students to be due to the fact that this new machine was quite perverse; dramatically different in structure from machines that they had worked with in the past. However, when the instruction manuals arrived, this turned out not to be the case: the new machine was very much like the others that the students had used.
Why did the students fail in their attempt to program this computer? One reason is that the physical states of the computer did not themselves provide any obvious organizational principles for determining how this machine would behave as an information processor. This is because very few of the physical states of a computer are relevant to the kind of information processing that the machine is actually carrying out. "In a given computer, only a minuscule subset of physically discriminable states are computationally discriminable" (Pylyshyn, 1984, p. 56). Churchland and Churchland (1990, p. 37) make a similar point in their reply to Searle's (1990) claim that any system capable of causing minds would have to have the causal power of the brain: "We presume that Searle is not claiming that a successful artificial mind must have all the causal powers of the brain, such as the power to smell bad when rotting, to harbor slow viruses such as kuru, to stain yellow with horseradish peroxidase and so forth. Requiring perfect parity would be like requiring that an artificial flying device lay eggs."
In short, while physical descriptions of information processing devices are going to be extremely useful, they will not be complete. First, the physical description of one device may not tell us anything about another information processor that is just as powerful, but is built from different stuff. Second, if you start with a physical description, you may have extreme difficulty getting a handle on information processing because only a small number of physical properties are germane to computing, and nature hasn't been kind enough to tell us exactly what these properties are.
Procedural Descriptions
Arbib (1972) argues for the necessity of organizational principles to guide the analysis of any complex information processor. What kinds of organizational principles were contained in the computer manuals that the Stanford graduate students failed to do without? One important set of principles would be some (nonphysical) description of the information processing steps that could be carried out by the computer. To be more specific, we could provide a very different explanation of how our Turing machine worked if instead of providing a description of its physical mechanism, we instead provided a description of the program or procedure that it was carrying out.
For a Turing machine, it turns out that there are two different kinds of procedural descriptions that we could provide. I'll call the first of these the architectural description, because in many respects it provides the most basic nonphysical account of the device. An architectural description of a Turing machine would be a description of that device's machine table. Note that all the machine table does is describe exactly the basic set of information processing steps (symbolic transformations of the tape) that characterize the device. It does not tell you anything about what the machine is built of -- indeed, the machine described in this vocabulary may never have been built at all! Nevertheless, this kind of description is very powerful. For example, if we know a Turing machine's table, and know a little bit more information about the machine (i.e., its current state and the current symbol that it is reading from the ticker tape) then we can predict exactly what the machine will do next. This ability allowed us to pretend to be the machine described in Figure 2.2.
However, architectural terms are not the only procedural ones that could be used to describe a particular Turing machine. This is because of the existence of the UTM. To provide a complete step-by-step account of a UTM's behavior, we would also have to describe the program that it was running (i.e., the particular Turing machine that the UTM was pretending to be). I'll call this the programming description. This is kind of description is going to be very useful because when the program is changed, the UTM will be doing something completely different, even though its architectural description was unchanged.
For the time being, I'm not going to make too much of the distinction between the architectural description and the programming description. I will, however, point the way to two related themes that are going to be fleshed out in greater detail in later chapters. First, the architectural description of a UTM is more fundamental than its programming description. If you wanted to build a UTM, your goal would be to create a physical device that implemented the UTM's machine table, not that implemented the UTM's programming description. As a result, when looking for relationships between different vocabularies, we would expect that stronger relationships should be found between physical descriptions and architectural descriptions than between physical descriptions and programming descriptions. Second (and related to the first), as far as cognitive science is concerned programming descriptions are going to be very powerful predictors of behavior. However, they are not going to suffice as explanations of behavior. To actually explain what might be going on in, say, a cognitive psychology experiment, some sort of architectural vocabulary is going to have to be employed.
Limitations Of Procedural Descriptions
One might think that if you had two types of descriptions of a Turing machine -- say, a physical description and an architectural description -- then you would be in a position to provide a precise explanation of this device to some other interested party. Unfortunately, this isn't going to be the case. While procedural descriptions capture regularities that physical descriptions don't, they themselves can't capture everything.
For example, let's go back to the question that I asked earlier about Figure 2.3. -- after following the machine table in Figure 2.2 to transform the tape in Figure 2.3a into the tape in Figure 2.3b, what exactly have you done? What question was the Turing machine that you simulated answering? What was the answer to this question that you produced? It turns out that to answer these two questions, you actually have to produce some interpretation of the tapes, as well as of the general procedure carried out by the Turing machine. Figure 2.5 is an attempt to help you come up with an answer to the question of what your simulation of the Figure 2.2 Turing machine actually meant. It provides some other examples of tapes as they would appear at the start of the machine's processing, and how the tapes would appear when the machine executed its "Stop" instruction. By looking at these tapes, as well as the pair illustrated in Figure 2.3, do you have a better idea about the meaning of the machine's actions?
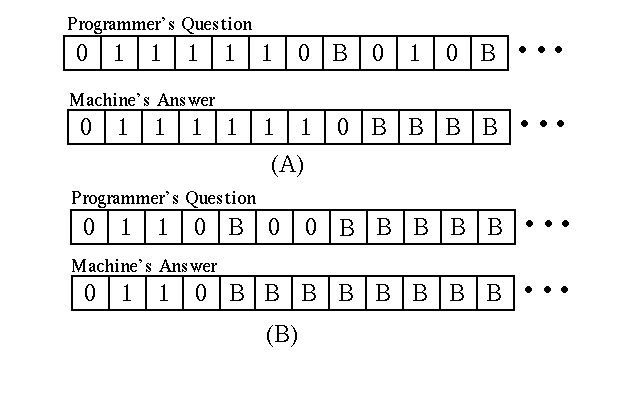
It turns out that the Turing machine table in Figure 2.2 is an architectural description of a device that takes any two integers and computes their sum (Adler, 1961, p. 24). Integers are represented in a slightly idiosyncratic unary notion. The symbol "0" is used to mark the beginning or the end of an integer quantity. The number of times the symbol "1" is duplicated between these punctuation marks gives the integer value being represented. So, the string "011110" represents the integer 4, and the string "011111111110" represents the integer 10. For this particular Turing machine, two integers are written on the tape and are separated by a blank. So, the tape "010B0110BBB..." represents the question "What is the sum of the integers 1 and 2?". At the end of processing, the machine's answer 3 is written as "01110".
The fantastic thing about information processing devices is that they are purely formal: they can carry out sophisticated computations by paying attention to the identity (or shape, or form) of the symbol on the tape without requiring to know what that particular symbol actually means, or requiring to know the meaning of what they are doing. As Haugeland (1985) wryly notes in his formalist's motto, if you take care of the syntax, then the semantics will take care of itself. This is part and parcel of the componential nature of the devices. Instead of requiring them to be extremely intelligent, understanding long and potentially complex strings of symbols, you simply require them to recognize a simple component of this string and respond to this symbol in a simple and definite way.
Unfortunately, a purely formal account of an information processor (i.e., either an architectural or a programming description) doesn't make it obvious how one should interpret a machine's actions or the symbols that the machine is processing. As a result, this descriptive vocabulary fails to capture some interesting regularities about information processors. To get a concrete sense of this, consider the architectural description of another Turing machine that is provided in Figure 2.6. At first glance, this description appears to be quite a bit different than the description of the other Turing machine in Figure 2.2, because the machines have different numbers of physical states, and because the machines respond to different numbers of symbols. Nevertheless, these machines are identical at a more abstract level, because both machine tables describe how a Turing machine can compute the sum of two integers. The difference between the two machines is that for the second one, "0's" are not used as punctuation marks in the unary notation for integer values.
Computational Descriptions
In order to capture the equivalence between the architectural descriptions provided by Figures 2.2 and 2.6, a third and even more abstract description of the Turing machine is required. This computational description would tell someone what kind of information processing problem is being solved by the machine without telling anything about the processing steps being used, or about how these processing steps are carried out by mechanical or physical processes. In very general terms, a computational description is an interpretation of what the system is computing. For instance, a computational description of the Turing machine in Figure 2.2 would simply say "this is an information processor that computes the sum of two integers".
In certain respects, computational descriptions appear to be relatively weak. However, they can capture generalizations that the other kinds of descriptions that we have discussed do not, and as a result give a different kind of predictive power. For example, let me tell you that I have a Turing machine that uses the unary notation from Figure 2.3 and that computes the product of two integers. If the machine is given the tape "0110B01110BBB...", what will the tape look like after the "Stop" instruction is executed? Notice that you can predict the behavior of this machine without building it, and without even knowing what its machine table would look like. All you need to know to predict the behavior is the scheme for interpreting the tape, and the knowledge that this particular machine is going to obey a particular semantic rule (i.e., multiplication).
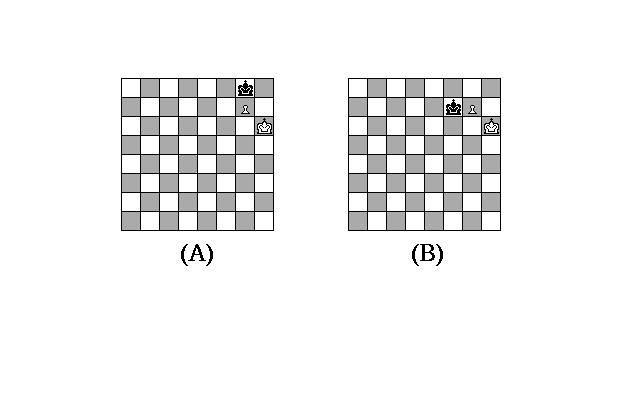
Figure 2.7 provides another example of the predictive power of computational descriptions. Imagine that I have a system that can be described computationally as a chess player. Thus, all you know about this system is that whatever it does, it will never violate the rules of chess. Let us imagine that the machine is playing black. Given the board position in the figure, what is Black's next move? If you know how to play chess, you will recognize this as an instance of Zugzwang: "the right of moving in Chess is at the same time an obligation" (Lasker, 1947, p. 17). As a result, by knowing what is going on computationally (i.e., that the laws of chess are being followed), you can predict that Black will move his King to KB2. No other move is possible.
Computational descriptions are generally formulated in some logical or mathematical notation, and as a result they provide extremely powerful nonexperimental methodologies for making discoveries about cognitive science. "The power of this type of analysis resides in the fact that the discovery of valid, sufficiently universal [computational] constraints leads to conclusions...that have the same permanence as conclusions in other branches of science" (Marr, 1982, p. 331). To illustrate this, let's bring our discussion of the Entscheidungsproblem to a close by presenting an extremely elegant proof (adapted from Minsky, 1963) that shows that there is no such thing as a Turing machine that could decide the truth of every possible mathematical statement.
Let's start by imagining that there is some Turing machine D that actually can resolve Hilbert's decidability question; our goal will be to show that this assumption must be false because it leads to a stark contradiction. Machine D works as follows: it takes a tape consisting of a description of some machine T (which we will represent as dT) as well as some data x for machine T to process. By examining this tape, D will tell you whether whether T will halt when it processes x, which tells us something about the truth of x if it is a mathematical statement. Now, x could be any string of symbols that D can read. One string of symbols that D can read is dT, so if we wanted to be perverse (and in this proof we do), we could ask D to tell us if machine T would halt or not when given its own description. (To introduce some notation, we could say that D(dT,dT) = "YES" if machine T would halt when processing the string dT, and D(dT,dT) = "NO" if machine T would not halt when processing the string dT).
Let's now try to simplify things by building a new Turing machine, which we will call M. M has the same ability as D, except it is a bit more special purpose. It only takes as input on its ticker tape the machine description dT, and then it only determines whether machine T would halt when given its own description. It has a few additional things built into it; for instance, we could imagine that it has some copying instructions that take the string dT and write it into the data part of the tape, after which M just behaves like D. (A nice mathematical notation for the relationship between machine D and machine M would be M(dT) = D(dT,dT)).
Machine M is going to have two different states in which it will execute its "Stop" instruction. For one of these, it will be stopping to say that machine T will not stop when processing the description of machine T. Let's leave this alone. For the other, it will be stopping to say that machine T will stop when processing the description of machine T. Let's break machine M at this point (to create machine M*) by causing it to go into an infinite loop at this point, when our nonbroken machine M would stop. Minksy (1963, p. 149) shows that breaking machine M in this particular way is very easy to do. So, if machine T will not stop when given its own description dT, then M* will stop. But if machine T will stop, M* will get stuck in an infinite loop, failing to halt.
Now, we can get nasty and move to proving that our initial assumption that machine D exists must be wrong. Let's ask M* to work on its own machine description dM*. If M*(dM*) stops, then it is saying that the operation M*(dM*) that is described on the tape will not stop -- an obvious contradiction. Similarly, if M*(dM*) does not stop, then it is saying that the operation M*(dM*) that is described on the tape does stop. These contradictions can lead to only one conclusion -- that there is a falsehood in the argument that we have been developing. Unfortunately, the only place where a falsehood could enter was our original assumption that machine D exists. Alas, we are forced to say that the answer to the Entscheidungsproblem is "no".
Limitations Of Computational Descriptions
As I attempted to show with the proof above, computational descriptions can be extremely useful. We were able to show how one could make an enormously powerful claim about what Turing machines can't do without building a machine, without writing a program, and without running an experiment. In cognitive science, though, by themselves computational descriptions may not be particularly powerful, as was the case with both physical and procedural descriptions. For example, with Figure 2.7, if all you know is that white and black pieces are being moved according to the rules of chess, then you can't predict with certainty that Black's forced move will result in a lost game. You can only make this prediction if you know a little bit more about how White chooses its next move, which is something that computational descriptions have nothing to say about, while procedural descriptions do. Similarly, you couldn't make any predictions about which addition machine (Figure 2.2 or 2.6) is faster without knowing the machine tables as well as the physical characteristics of the two devices.
The Tri-Level Hypothesis
To summarize our discussion of what you can say about Turing machines, I have argued that there are three very general vocabularies that can be used to describe these devices (physical, procedural, computational). Each of these vocabularies describes certain things (or makes certain predictions) that the other two vocabularies do not. However, none of these vocabularies provide a complete account of information processors.
Some researchers (e.g., Dennett, 1978), while in agreement about the applicability of these three different descriptive vocabularies, would argue that their use has only heuristic value. From this perspective, there is no obligation to use all three vocabularies to describe a single system. Other researchers (e.g., Churchland, 1988) would argue that the goal of cognitive science should be to eliminate computational and procedural terms, reducing them to purely physical concepts. I do not believe that either of these approaches are correct. I've tried to use some informal examples above to show that if you are missing one or more of the descriptions, then you are literally saying less about information processing, because there are certain predictions that you cannot make without using all three types of vocabularies.
This sense that a complete explanation of information processing will require physical, procedural, and computational descriptions is in fact characteristic of cognitive science. "There is a natural theoretical domain within psychology which corresponds roughly to what we pretheoretically call cognition, in which the principal generalizations covering behavior occur at three autonomous levels of description, each conforming to different principles" (Pylyshyn, 1984, p. 259). Without all three vocabularies, explanation vanishes into incomplete description. Furthermore, the need for these three vocabularies is necessitated by the fundamental, complicated nature of information processors. I would strongly argue that if you can omit one of the vocabularies without losing any predictive or explanatory power, then the system that you are explaining is not an information processor. For example, while it is perfectly appropriate for philosophers to ascribe beliefs to thermostats to make particular points, it is important to realize that assuming that your thermostat believes that the room is hot doesn't tell us anything more about it that we didn't already know from a physical description. For similar reasons, we don't purchase any new explanatory power by claiming that falling rocks are actively computing their trajectories.
I think that we are now in a position to convert the view that has been developing over the past few pages into a piece of cognitive science dogma, which we will call the tri-level hypothesis. Cognitive scientists believe that the mind is an information processor. As a result, a cognitive phenomenon must be explained by (1) describing it using a physical vocabulary, a procedural vocabulary, and a computational vocabulary, and (2) finding principled relationships between these three qualitatively different accounts.
Classical Cognitive Science
The tri-level hypothesis is true of all cognitive science. However, within cognitive science different traditions have emerged which can be differentiated with respect to the extent that other properties of the Turing machine have been incorporated into cognitive theory. Later chapters will discuss one of these traditions, called connectionism, which has moved in important ways away from the Turing machine description. This final section of this chapter briefly describes the other, classical cognitive science, which currently represents the status quo tradition in the field.
Classical cognitive science not only assumes that the tri-level hypothesis is valid, but it uses this hypothesis in a particular methodological manner. Let's imagine that, like the the Stanford graduate students, a classical cognitive scientist is presented with the task of explaining an unknown information processor. How will this task be approached? In general, classical cognitive scientists adopt a very specific top-down strategy (Marr, 1982). First, they attempt to describe the system with the computational vocabulary. Second, they attempt to use the programming vocabulary, working their way towards the architectural description. Finally, they attempt a physical description. There are a number of reasons for adopting this top-down strategy.
First, with this approach a more abstract vocabulary provides Arbib's (1972) organizational principles, which guide the analysis with the less abstract vocabulary. Second, basically restating the first, this approach defines a particular methodological practice called functional analysis (e.g., Cummins, 1983) which has been enormously productive in cognitive science. Third, moving from more to less abstract descriptive vocabularies is viewed by classical cognitive scientists as providing deeper understanding. "It is not that one gains precision in descending the explanatory reduction hierarchy. What one gains is a deeper, more general, and therefore more complete, explanation" (Pylyshyn, 1979, p. 428). Finally, as one moves in this direction, one proceeds from computational claims that should be true of all information processors to physical claims that are likely to only be true of a small number of information processors, one of which is the system under study. Classical cognitive scientists also take to heart some additional distinctions that are made explicit in the Turing machine formulation of information processing. In general, they endorse a sharp distinction between the processes or rules that are manipulating information, and the symbols that actually represent the information being manipulated. This is the distinction between the tape and the head of the Turing machine. As well, they also endorse the sharp distinction between a program that can be represented in memory and data that can be manipulated by this program. This is the distinction between a machine description and other symbol strings that are processed by the UTM. Connectionists have attempted to abandon these sharp distinctions between rules and symbols (see Dawson & Schopflocher, 1992).
Conversations And Cognitive Science
In the previous chapter, I argued that the information processing assumption provided some common ground that permitted cognitive scientists to have fruitful conversations with one another, even if different individuals had widely different research backgrounds. Now that we have talked at great length about a particular view of what information processing is, we can strengthen this thread a little bit by suggesting why in addition to being possible, these conversations are going to be necessary.
This chapter has been an extended argument that when a cognitive scientist starts with the assumption that cognition is information processing, then he or she must apply the tri-level assumption. Consider what that means for human cognition. We are going to require a mature neuroscience to provide the physical account. We are going to require many technical results from psychology and linguistics to provide enough empirical details in which to ground procedural descriptions. We are going to require computer scientists and philosophers to provide adequate computational descriptions of the information processing that is being carried out. Finally, we are going to require conversations among all of these different researchers in order to put all of this together in a complete package in which all of the relationships among the vocabularies are spelled out. A successful cognitive science is going to require a lot of teamwork.
In short, the assumption that cognition is information processing forces the tri-level hypothesis upon us, and this in turn requires cognitive science to be interdisciplinary. In my opinion, this is why I find cognitive science such an exciting and attractive field. Its basic assumptions force you to look at one problem from a number of completely different angles, allow you to use an enormous variety of methodologies to solve these problems, and require you to start talking about these problems and methodologies with colleagues from a variety of disciplines.
Chapter Notes
References